What is the number of triangles that can be formed whose vertices are the vertic

CuriousTab

Home Aptitude

Discussion

Home ‣ Non Verbal Reasoning ‣ Analytical Reasoning See What Others Are Saying!

Question
What is the number of triangles that can be formed whose vertices are the vertices of an octagon but have only one side common with that of octagon?
Options
A. 64
B. 32
C. 24
D. 16

Correct Answer

32

Explanation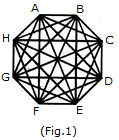

When the triangles are drawn in an octagon with vertices same as those of the octagon and having one side common to that of the octagon, the figure will appear as shown in (Fig. 1).

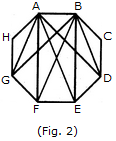
What is the number of triangles that can be formed whose vertices are the vertices of an octagon but

Now, we shall first consider the triangles having only one side AB common with octagon ABCDEFGH and having vertices common with the octagon (See Fig. 2).Such triangles are ABD, ABE, ABF and ABG i.e. 4 in number.

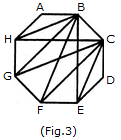
What is the number of triangles that can be formed whose vertices are the vertices of an octagon but

Similarly, the triangles having only one side BC common with the octagon and also having vertices common with the octagon are BCE, BCF, BCG and BCH (as shown in Fig. 3). i.e. There are 4 such triangles.

This way, we have 4 triangles for each side of the octagon. Thus, there are 8 x 4 = 32 such triangles.