 |
CuriousTab |
CuriousTab
Discussion
Home ‣ Non Verbal Reasoning ‣ Analytical Reasoning See What Others Are Saying!
- Question
Find the number of triangles in the given figure.
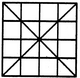
Options- Correct Answer
- 48
ExplanationThe figure may be labelled as shown.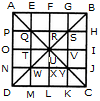
The simplest triangles are APQ, AEQ, QTU, QRU, BGS, BHS, RSU, SUV, TUW, UWX, NWD, WDM, UVY, UXY, JCY and YKC i.e. 16 in number.
The triangles composed of two components each are QUW, QSU, SYU and UWY i.e. 4 in number.
The triangles composed of three components each are AOU, AFU, FBU, BIU, UIC, ULC, ULD and OUD i.e. 8 in number.
The triangles composed of four components each are QYW, QSW, QSY and SYW i.e. 4 in number.
The triangles composed of six components each are AUD, ABU, BUC and DUC i.e. 4 in number.
The triangles composed of seven components each are QMC, ANY, EBW, PSD, CQH, AGY, DSK and BJW i.e. 8 in number.
The triangles composed of twelve components each are ABD, ABC, BCD and ACD i.e. 4 in number.
Thus, there are 16 + 4 + 8 + 4 + 4 + 8 + 4 = 48 triangles in the figure.
More questions
- 8. Select the alternative which represents three out of the five alternative figures which when fitted into each other would form a equilateral triangle.
Options
Discuss
Correct Answer: 234
Explanation:
- 9. Group the given figures into three classes using each figure only once.
Options
Discuss
Correct Answer: 1,2,3 ; 4,5,6 ; 7,8,9
Explanation:
1, 2, 3 are figures composed of two straight lines.4, 5, 6 are figures composed of three straight lines.
7, 8, 9 are figures composed of four straight lines.
- 10. Find out which of the figures (1), (2), (3) and (4) can be formed from the pieces given in figure (X).
Options
Discuss
Correct Answer: 3
Explanation:
Comments
There are no comments.
- 8. Select the alternative which represents three out of the five alternative figures which when fitted into each other would form a equilateral triangle.