Find the number of triangles in the given figure. 27 25 23 21 The figure may be

CuriousTab

CuriousTab

Home Aptitude

Discussion

Home ‣ Non Verbal Reasoning ‣ Analytical Reasoning See What Others Are Saying!

Question
Find the number of triangles in the given figure.
Options
A. 27
B. 25
C. 23
D. 21

Correct Answer

27

Explanation

The figure may be labelled as shown.

Find the number of triangles in the given figure. 27 25 23 21 The figure may be labelled as shown.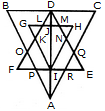 T

The simplest triangles are GLK, DLJ, DJM, HMN, QRE, IRA, IPA and FPO i.e. 8 in number.

The triangles having two components each are BDO, CDQ, DLM, PRA, KFI, NEI, HJI, GJI, DKI and DNI i.e. 10 in number.

The triangles having four components each are DIE, DFI, DOA, DQA andGHI i.e. 5 in number.

The triangles having six components each are DCA and DBA i.e. 2 in number.

DEF is the only triangle having eight components.

ABC is the only triangle having twelve components.

Thus, there are 8+10+ 5 + 2+1 + 1 = 27 triangles in the figure.

More questions

1. Find out the next series from the answer figures (1, 2, 3, 4, 5) that follows the sequence of the questions figures:
Options
A. 1
B. 2
C. 3
D. 4

3. Choose the figure which is different from the rest.

(1) (2) (3) (4) (5)
Options
A. 1
B. 2
C. 3
D. 4
E. 5

4. Choose the figure which is different from the rest.

(1) (2) (3) (4) (5)
Options
A. 1
B. 2
C. 3
D. 4
E. 5

5. Choose the figure which is different from the rest.

(1) (2) (3) (4) (5)
Options
A. 1
B. 2
C. 3
D. 4
E. 5

6.
Select the figure which is different from the rest.
Options
A. 1
B. 2
C. 3
D. 4

9.
Find out from the four alternatives as how the pattern would appear when the transparent sheet is folded at the dotted line.
Options
A. (a)
B. (b)
C. (c)
D. (d)

10.
In this question, among the four answer figures, which figure can be formed from the cut? pieces given below in the question figure.
Options
A. 1
B. 2
C. 3
D. 4

Comments

There are no comments.

More in Non Verbal Reasoning: