Discussion
Home ‣ Non Verbal Reasoning ‣ Analytical Reasoning See What Others Are Saying!
- Question
A university library budget committee must reduce exactly five of eight areas of expenditure?I, J, K, L, M, N, O and P?in accordance with the following conditions: If both I and O are reduced, P is also reduced. If L is reduced, neither N nor O is reduced. If M is reduced, J is not reduced. Of the three areas J, K, and N exactly two are reduced. Question : If both K and N are reduced, which one of the following is a pair of areas neither of which could be reduced?
Options- A. I, L
- B. J, L
- C. J, M
- D. I, J
- Correct Answer
- J, L
ExplanationThis question concerns a committee's decision about which five of eight areas of expenditure to reduce. The question requires you to suppose that K and N are among the areas that are to be reduced, and then to determine which pair of areas could not also be among the five areas that are reduced.
The fourth condition given in the passage on which this question is based requires that exactly two of K, N, and J are reduced. Since the question asks us to suppose that both K and N are reduced, we know that J must not be reduced:
Reduced :: K, N
Not reduced :: JThe second condition requires that if L is reduced, neither N nor O is reduced. So L and N cannot both be reduced. Here, since N is reduced, we know that L cannot be. Thus, adding this to what we've determined so far, we know that J and L are a pair of areas that cannot both be reduced if both K and N are reduced:
Reduced :: K, N
Not reduced :: J, LAnswer choice (B) is therefore the correct answer.
- 1. In a solid cube which is made up of 27 small cubes, two opposite sides are painted red, two painted yellow and the other two with white. How many cubes have two colours?
Options- A. 8
- B. 12
- C. 16
- D. 24 Discuss
- 2. Choose the figure which is different from the rest.
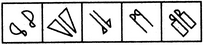 (1) (2) (3) (4) (5)
(1) (2) (3) (4) (5)
Options- A. 1
- B. 2
- C. 3
- D. 4
- E. 5 Discuss
- 3. Select the alternative in which the specified components of the key figure (X) are found.
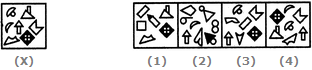
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 4. Choose the set of figures which follows the given rule.
Rule: As the circle decreases in size, its sectors increase in number.
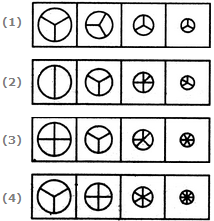
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 5. Identify the figure that completes the pattern.
 (X) (1) (2) (3) (4)
(X) (1) (2) (3) (4)
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 6. Choose a figure which would most closely resemble the unfolded form of Figure (Z).
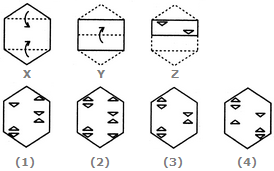
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 7. Select a suitable figure from the four alternatives that would complete the figure matrix.
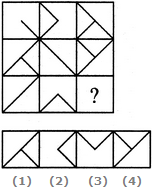
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 8. Select the alternative which represents three out of the five alternative figures which when fitted into each other would form a equilateral triangle.

Options- A. 234
- B. 123
- C. 345
- D. 235 Discuss
- 9. Choose the figure which is different from the rest.
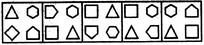 (1) (2) (3) (4) (5)
(1) (2) (3) (4) (5)
Options- A. 1
- B. 2
- C. 3
- D. 4
- E. 5 Discuss
- 10. Group the given figures into three classes using each figure only once.

Options- A. 3,4,9 ; 5,7,8 ; 1,2,6
- B. 1,5,6 ; 2,4,8 ; 3,7,9
- C. 4,6,8 ; 3,5,7 ; 1,2,9
- D. 1,2,7 ; 3,5,9 ; 4,6,8 Discuss
More questions
Correct Answer: 12
Explanation:
Correct Answer: 3
Explanation:
Correct Answer: 4
Correct Answer: 4
Correct Answer: 3
Explanation:

Correct Answer: 3
Correct Answer: 2
Explanation:
Correct Answer: 123
Explanation:
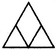
Correct Answer: 4
Explanation:
Correct Answer: 1,2,7 ; 3,5,9 ; 4,6,8
Explanation:
3, 5, 9 have one element placed inside a different element.
4, 6, 8 have two different elements attached to each other.
Comments
There are no comments.Programming
Copyright ©CuriousTab. All rights reserved.
