 |
CuriousTab |
CuriousTab
Discussion
Home ‣ Non Verbal Reasoning ‣ Mirror Images See What Others Are Saying!
- Question
Options- Correct Answer
- 4
ExplanationAccording to given question figure ,
we can say that the mirror image always be opposite the original image across the given line. Given image will become opposite in mirror across the given line MN. - 2. Select a figure from amongst the Answer Figures which will continue the same series as established by the five Problem Figures.
Problem Figures: Answer Figures:
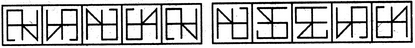(A) (B) (C) (D) (E) (1) (2) (3) (4) (5)
Options
Discuss
- 3. Find the number of triangles in the given figure.
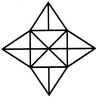
Options
Discuss
- 4. Find out which of the figures (1), (2), (3) and (4) can be formed from the pieces given in figure (X).
Options
Discuss
- 5. Select a suitable figure from the Answer Figures that would replace the question mark (?).
Problem Figures: Answer Figures:
(A) (B) (C) (D) (1) (2) (3) (4) (5)
Options
Discuss
- 6. Select a figure from amongst the Answer Figures which will continue the same series as established by the five Problem Figures.
Problem Figures: Answer Figures:
(A) (B) (C) (D) (E) (1) (2) (3) (4) (5)
Options
Discuss
- 7. Choose the alternative which is closely resembles the water-image of the given combination.
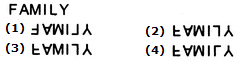
Options
Discuss
- 8. Select the figure which satisfies the same conditions of placement of the dots as in Figure-X.
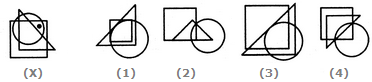
Options
Discuss
- 10. Select a suitable figure from the Answer Figures that would replace the question mark (?).
Problem Figures: Answer Figures:
(A) (B) (C) (D) (1) (2) (3) (4) (5)
Options
Discuss
More questions
Correct Answer: 4
Explanation:
The figure gets laterally inverted and vertically inverted alternately.
Correct Answer: 28
Explanation:
The figure may be labelled as shown.
The simplest triangles are AEI, AIH, BEJ, BJF, CFK, CKG, DGL, DLH, EOJ, FOJ, FOG, LOG, HOL and HOE i.e. 14 in number.
The triangles composed of two components each are EAH, FBE, BEO, EOF, BFO, FCG, GDH, HOD, HOG and GOD i.e. 10 in number.
The triangles composed of three components each are EFH, EHG, FGH and EFG i.e. 4 in number.
Thus, there are 14 + 10 + 4 = 28 triangles in the given figure.
Correct Answer: 2
Correct Answer: 1
Explanation:
The figure gets vertically inverted and the two vertical lines inside the figure get rotated through 90
o.
Correct Answer: 4
Explanation:
All the elements move half-a-side of the square boundary in ACW direction in each step. Also, first, third and fifth elements are replaced by new elements in one step and second, fourth and sixth elements are replaced by new elements in the next step. The two steps are repeated alternately.
Correct Answer: 4
Correct Answer: 4
Explanation:
In fig. (X), the dot is contained in the region common to the square and the circle only. Out of the four alternatives, only fig. (4) contains a region common to the square and the circle only.
Correct Answer: 2
Explanation:
As many pins are introduced inside the figure as the number of sides of the figure. These pins start from the centre of the figure and have their heads pointing towards the sides of the figure.
Comments
There are no comments.