Discussion
Home ‣ Non Verbal Reasoning ‣ Analogy See What Others Are Saying!
- Question
Four pairs of flower pots are given below. Among them only one pair is similar in all respects. Identify the pair numbers which represent that pair:

Options- A. 1 - 5
- B. 3 - 6
- C. 5 - 8
- D. 4 - 7
- Correct Answer
- 5 - 8
ExplanationFigures (5) and 8 are similar.
- 1. Choose the correct mirror image of the given figure (X) from amongst the four alternatives.
 (X) (1) (2) (3) (4)
(X) (1) (2) (3) (4)
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 2. NA
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 3. GLOBE
Options- A. .
- B. .
- C. .
- D. . Discuss
- 4. Group the given figures into three classes using each figure only once.

Options- A. 7,8,9 ; 2,4,3 ; 1,5,6
- B. 1,3,2 ; 4,5,7 ; 6,8,9
- C. 1,6,8 ; 3,4,7 ; 2,5,9
- D. 1,6,9 ; 3,4,7 ; 2,5,8 Discuss
- 5. Find the question mark
? figure from answer figure:

Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 6. Select a suitable figure from the Answer Figures that would replace the question mark (?).
Problem Figures: Answer Figures:
 (A) (B) (C) (D) (1) (2) (3) (4) (5)
(A) (B) (C) (D) (1) (2) (3) (4) (5)
Options- A. 1
- B. 2
- C. 3
- D. 4
- E. 5 Discuss
- 7. Select a suitable figure from the Answer Figures that would replace the question mark (?).
Problem Figures: Answer Figures:
 (A) (B) (C) (D) (1) (2) (3) (4) (5)
(A) (B) (C) (D) (1) (2) (3) (4) (5)
Options- A. 1
- B. 2
- C. 3
- D. 4
- E. 5 Discuss
- 8. Choose a figure which would most closely resemble the unfolded form of Figure (Z).
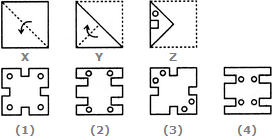
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 9. Find the question mark ? figure from answer figure.
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 10. NA
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
More questions
Correct Answer: 4
Correct Answer: 2
Explanation:
NA
Correct Answer: .
Explanation:
Answer A
Correct Answer: 1,6,9 ; 3,4,7 ; 2,5,8
Explanation:
1, 6, 9, are all triangles.
3, 4, 7 are all four-sided figures.
2, 5, 8 are all five-sided figures.
Correct Answer: 2
Explanation:
From first figure to second figure the diagonals are deleted and both the dots are arranged vertically.
Correct Answer: 1
Explanation:
The symbols move in the sequence
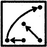 . Also, the arrow rotates 135
oACW; the trapezium gets vertically inverted and the pin-shaped symbol rotates 90
oCW.
. Also, the arrow rotates 135
oACW; the trapezium gets vertically inverted and the pin-shaped symbol rotates 90
oCW.
 . Also, the arrow rotates 135
oACW; the trapezium gets vertically inverted and the pin-shaped symbol rotates 90
oCW.
. Also, the arrow rotates 135
oACW; the trapezium gets vertically inverted and the pin-shaped symbol rotates 90
oCW.
Correct Answer: 2
Explanation:
The upper element rotates through 180
o and its head gets inverted. The lower element gets vertically inverted.
Correct Answer: 3
Correct Answer: 4
Explanation:
The first figure is bigger in each unit.
Correct Answer: 4
Explanation:
NA
Comments
There are no comments.Programming
Copyright ©CuriousTab. All rights reserved.
