Discussion
Home ‣ Non Verbal Reasoning ‣ Series See What Others Are Saying!
- Question
- Find out the next series from the Answer Figure that follows the sequence of the Question Figure.:

Options- A. 1
- B. 2
- C. 3
- D. 4
- Correct Answer
- 3
ExplanationIn one step, the arrow and the small line segment turn to other side of the more line and in the next figure.
- 1.
How many triangles are there in the question figure?

Options- A. 16
- B. 23
- C. 26
- D. 31 Discuss
- 2.
In these tests find which code matches the shape or pattern given at the end of each question.

Options- A. BF
- B. GB
- C. BG
- D. CG Discuss
- 3. Find out how will the key figure (X) look like after rotation.
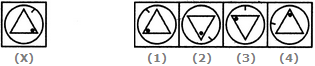
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 4. Choose a figure which would most closely resemble the unfolded form of Figure (Z).
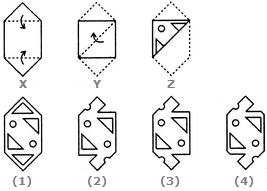
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 5. A piece of paper is folded and punched as shown below. From the given responses indicate how it will appear when opened.
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 6. '
Options- A. (a)
- B. (b)
- C. (c)
- D. (d) Discuss
- 7. Three positions of a dice are given. Based on them find out which number is found opposite the number 2 in the given cube.

Options- A. 6
- B. 5
- C. 3
- D. 1 Discuss
- 8. Choose the correct water image of the given figure (X) from amongst the four alternatives.

Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 9. Choose the alternative which is closely resembles the mirror image of the given combination.

Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 10. Count the number of convex pentagons in the adjoining figure.
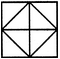
Options- A. 16
- B. 12
- C. 8
- D. 4 Discuss
More questions
Correct Answer: 31
Explanation:
Correct Answer: BG
Explanation:
Something should end with M
Correct Answer: 4
Correct Answer: 4
Correct Answer: 3
Explanation:
NA
Correct Answer: (b)
Explanation:
NA
Correct Answer: 6
Explanation:
From figures (i) and (ii), we conclude that the numbers 1, 4, 3 and 5 lie adjacent to the number 6. Clearly, the number 2 lies opposite 6 and conversely 6 lies opposite 2.
Correct Answer: 1
Correct Answer: 2
Correct Answer: 12
Explanation:
A convex pentagon has no angles pointing inwards. More precisely, no internal angles can be more than 180°.
The figure may be labelled as shown.
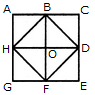
The pentagons in the figure, are ABDFH, CDFHB, EFHBD, GHBDF, ACDFG, CEFHA, EGHBC, GABDE, BDEGH, DFGAB, FHACD and HBCEF. Clearly, these are 12 in number.
Comments
There are no comments.Programming
Copyright ©CuriousTab. All rights reserved.
