Discussion
Home ‣ Non Verbal Reasoning ‣ Cubes and Dice See What Others Are Saying!
- Question
- How many cubes are painted with red, blue, green and black?
Options- A. 8
- B. 2
- C. 1
- D. None of these
- Correct Answer
- None of these
ExplanationHere on each face 6 x 6 = 36 cubes that are painted with one colour.
None of the cubes can be painted in four faces. - 1. Choose the alternative which is closely resembles the water-image of the given combination.

Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 2. Identify the two figures from the given figures which are identical:
Options- A. 1 - 3
- B. 4 - 6
- C. 2 - 4
- D. 3 - 5 Discuss
- 3. Which answer figure will complete the pattern in the question figure?
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 4. Select a suitable figure from the Answer Figures that would replace the question mark (?).
Problem Figures: Answer Figures:
 (A) (B) (C) (D) (1) (2) (3) (4) (5)
(A) (B) (C) (D) (1) (2) (3) (4) (5)
Options- A. 1
- B. 2
- C. 3
- D. 4
- E. 5 Discuss
- 5. Find the number of triangles in the given figure.
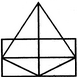
Options- A. 11
- B. 13
- C. 15
- D. 17 Discuss
- 6. Select a suitable figure from the Answer Figures that would replace the question mark (?).
Problem Figures: Answer Figures:
 (A) (B) (C) (D) (1) (2) (3) (4) (5)
(A) (B) (C) (D) (1) (2) (3) (4) (5)
Options- A. 1
- B. 2
- C. 3
- D. 4
- E. 5 Discuss
- 7. Find the missig figure of the series from the given responses:

Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 8. Choose the correct mirror image of the given figure (X) from amongst the four alternatives.
 (X) (1) (2) (3) (4)
(X) (1) (2) (3) (4)
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 9. Four corners of a rectangular shaded paper are folded as shown in the figure. Find out from the alternative answers how the folded figure would look.
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 10. A square sheet of paper is folded and punched as shown below. How will it look when opened?
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
More questions
Correct Answer: 2
Correct Answer: 2 - 4
Explanation:
Figures 2 and 4 are identical.
Correct Answer: 3
Explanation:
NA
Correct Answer: 4
Explanation:
Correct Answer: 15
Explanation:
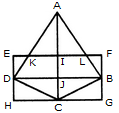
The simplest triangles are AKI, AIL, EKD, LFB, DJC, BJC, DHC and BCG i.e. 8 in number.
The triangles composed of two components each are AKL, ADJ, AJB and DBC i.e. 4 in number.
The triangles composed of the three components each are ADC and ABC i.e. 2 in number.
There is only one triangle i.e. ADB composed of four components.
Thus, there are 8+ 4 + 2 + 1= 15 triangles in the figure.
Correct Answer: 3
Explanation:
Correct Answer: 3
Explanation:
As per the given figure in above question, we can say that
From first figure to second figure the circle and the rectangle interchange positions and the upper shaded square moves to the lower side.
Thus , figure ( 3 ) will come on the place of ? in question figure .As shown in answer figures .
Correct Answer: 3
Correct Answer: 1
Explanation:
NA
Correct Answer: 2
Explanation:
NA
Comments
There are no comments.Programming
Copyright ©CuriousTab. All rights reserved.
