 |
CuriousTab |
CuriousTab
Discussion
Home ‣ Non Verbal Reasoning ‣ Cubes and Dice See What Others Are Saying!
- Question
Options- Correct Answer
- 33
ExplanationOnly two faces are coloured is when cubes are at the edges (baring the corner cubes)
If no cubes have been removed then on each edges we will get 3 cubes that has exactly 2 faces coloured, hence total number of such cubes = 12 x 3 = 36, because we have 12 edges.
Out of these 3 cubes are removed hence required number of cubes = 36 - 3 = 33 - 1. Select a figure from amongst the Answer Figures which will continue the same series as established by the five Problem Figures.
Problem Figures: Answer Figures:
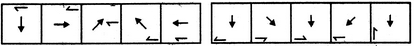(A) (B) (C) (D) (E) (1) (2) (3) (4) (5)
Options
Discuss
- 2. Select a suitable figure from the Answer Figures that would replace the question mark (?).
Problem Figures: Answer Figures:
(A) (B) (C) (D) (1) (2) (3) (4) (5)
Options
Discuss
- 3. Select a suitable figure from the Answer Figures that would replace the question mark (?).
Problem Figures: Answer Figures:
(A) (B) (C) (D) (1) (2) (3) (4) (5)
Options
Discuss
- 4. Select a suitable figure from the Answer Figures that would replace the question mark (?).
Problem Figures: Answer Figures:
(A) (B) (C) (D) (1) (2) (3) (4) (5)
Options
Discuss
- 6. Select a suitable figure from the Answer Figures that would replace the question mark (?).
Problem Figures: Answer Figures:
(A) (B) (C) (D) (1) (2) (3) (4) (5)
Options
Discuss
- 7. Select a suitable figure from the Answer Figures that would replace the question mark (?).
Problem Figures: Answer Figures:
(A) (B) (C) (D) (1) (2) (3) (4) (5)
Options
Discuss
- 8. Select a suitable figure from the Answer Figures that would replace the question mark (?).
Problem Figures: Answer Figures:
(A) (B) (C) (D) (1) (2) (3) (4) (5)
Options
Discuss
- 9. Identify the figure that completes the pattern.
(X) (1) (2) (3) (4)
Options
Discuss
More questions
Correct Answer: 1
Explanation:
The central arrow rotates 90
oACW and 45
oCW alternately. The half-arrow moves half-a-side of the square boundary in a CW direction and its head turns to the other side of the line in each step.
Correct Answer: 1
Explanation:
The upper element is converted to an element similar to the lower elements and each one of the lower elements is converted to an element similar to the upper element.
Correct Answer: 4
Explanation:
The black leaf rotates 135
oACW and white leaf rotates 90
oACW
Correct Answer: 3
Explanation:
The two elements interchange positions; the element that reaches the LHS position gets vertically inverted and the element that reaches the RHS position, rotates 90
oACW.
Correct Answer: 4
Explanation:
The set of three pins gets vertically inverted and moves to the lower-right position; the triangle rotates 90
oACW; the third element rotates 45
oACW and moves to the upper-left position. The dot in this element moves to the adjacent portion in a CW direction.
Correct Answer: 4
Explanation:
The figure rotates through 90
o the two parts get separated along the dividing line; each part gets rotated through 180
o and these two parts are joined together by a black circle.
Correct Answer: 4
Explanation:
The arrow rotates 135
oCW and the remaining part of the figure rotates 90
oACW.
Correct Answer: 2
Explanation:
Comments
There are no comments.