Discussion
Home ‣ Non Verbal Reasoning ‣ Cubes and Dice See What Others Are Saying!
- Question
- What is the ratio of maximum and minimum number of cuboids with red colour on them?
Options- A. 18 : 7
- B. 18 : 5
- C. 16 : 5
- D. None of these
- Correct Answer
- 18 : 5
ExplanationFor least number of cuts 120 = 4 x 5 x 6 i.e number of cuts must be 3, 4 and 5 in three planes in this case number of cubes on a face is either 6 x 5 = 30 or 6 x 4 = 24 or 4 x 5 = 20 cubes . And number of cuboids on an edge is 4 or 5 or 6
Maximum number of cuboid with red colour is possible when cube is painted with red colour in 3 sides with minimum number of common edges (which is equal to 2)
Hence required maximum value is 6 (5 + 5 + 4 - 2) = 72
For minimum number of such cuboid Red colour is used only once and minimum number of cubes in that case is 20
Hence required ratio is 72 : 20 = 18 : 5 - 1. Find out the next series from the answer figures
(1, 2, 3, 4, 5) that follows the sequence of the questions figures:

Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 2. Choose the alternative which is closely resembles the mirror image of the given combination.

Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 3. Choose the figure which is different from the rest.
 (1) (2) (3) (4) (5)
(1) (2) (3) (4) (5)
Options- A. 1
- B. 2
- C. 3
- D. 4
- E. 5 Discuss
- 4. Choose the figure which is different from the rest.
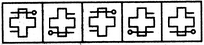 (1) (2) (3) (4) (5)
(1) (2) (3) (4) (5)
Options- A. 1
- B. 2
- C. 3
- D. 4
- E. 5 Discuss
- 5. Choose the figure which is different from the rest.
 (1) (2) (3) (4) (5)
(1) (2) (3) (4) (5)
Options- A. 1
- B. 2
- C. 3
- D. 4
- E. 5 Discuss
- 6. Select the figure which is different from the rest.
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 7. '
Options- A. (a)
- B. (b)
- C. (c)
- D. (d) Discuss
- 8. NA
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 9. Find out from the four alternatives as how the pattern would appear when the transparent sheet is folded at the dotted line.
Options- A. (a)
- B. (b)
- C. (c)
- D. (d) Discuss
- 10. In this question, among the four answer figures, which figure can be formed from the cut? pieces given below in the question figure.
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
More questions
Correct Answer:
Explanation:
This is the path of lower figure whereas the figures follows the above path and
changes the position in 90 degree up n down manner.
Correct Answer: 2
Correct Answer: 1
Explanation:
Correct Answer: 5
Explanation:
Correct Answer: 1
Explanation:
Correct Answer: 4
Explanation:
In figure (4) the design (T) is smaller and it does not intersect the other design. So , option D is required answer .
Correct Answer: (a)
Explanation:
NA
Correct Answer: 2
Explanation:
NA
Correct Answer: (a)
Explanation:
Answer A
Correct Answer: 3
Explanation:
NA
Comments
There are no comments.Programming
Copyright ©CuriousTab. All rights reserved.
