Discussion
Home ‣ Non Verbal Reasoning ‣ Cubes and Dice See What Others Are Saying!
- Question
- How many of the cubes have 2 faces painted?
Options- A. 23
- B. 29
- C. 44
- D. None of these
- Correct Answer
- 44
ExplanationOut of 6 faces of 5 faces are exposed and those were painted.
Number of vertices with three faces exposed (Painted) is 4
Number of vertices with 2 faces exposed (Painted) is 4
Number of vertices with 1 faces exposed (Painted) is 0
Number of vertices with 0 faces exposed (Painted) is 0
Number of sides with 2 sides exposed (Painted) is 8
Number of sides with 1 sides exposed (Painted) is 4
Number of sides with no sides exposed (Painted) is 0
From the above observation:
Number of cubes with 3 faces Painted is 4
Number of cubes with 2 faces Painted is given by sides which is exposed from two sides, out of 8 such edges 4 vertical edges will give us 6 cubes per edge and 4 edges from top surface will give us 5 such cubes from each edge and required number of cubes is 6 x 4 + 4 x 5 = 44.
Number of cubes with 1 face Painted is given by faces which is exposed from one sides four vertical faces will give us 6 x 5 = 30 cubes per face and top face will give us 5 x 5 = 25 and required number of cubes is 30 x 4 + 25 x 1 = 145
Number of cubes with 0 face Painted is given by difference between total number of cubes - number of cubes with at least 1 face painted = 343 - 4 - 44 - 145 = 150
In other words number of cubes with 0 painted is 6 x 5 x 5 = 150
From the above explanation number of the cubes with 0 faces painted is 150.
From the above explanation number of the cubes with 2 faces painted is 44. - 1. A piece of paper is folded and a cut is made a shown below. From the given responses indicate how it will appear when opened.
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 2. Form the correct pattern with the segments given.
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 3. Find out from the four alternatives as how the pattern would appear when the transparent sheet is folded at the dotted line.
Options- A. (a)
- B. (b)
- C. (c)
- D. (d) Discuss
- 4. Find the odd one out.
Options- A. 4
- B. 1
- C. 2
- D. 3 Discuss
- 5. Choose the alternative which is closely resembles the water-image of the given combination.

Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
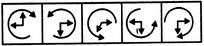
- 6. Choose the figure which is different from the rest.
 (1) (2) (3) (4) (5)
(1) (2) (3) (4) (5)
Options- A. 1
- B. 2
- C. 3
- D. 4
- E. 5 Discuss
- 7. If a mirror is placed on the line MN,then which of the answer figures is the right image, of the given figure?
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 8. Find the question mark ? figure from answer figure.
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 9. The figure above is a drawing of pile of Blocks. When taken apart, how many blocks would be there?
Options- A. 15
- B. 14
- C. 10
- D. 5 Discuss
- 10. A dice is numbered from 1 to 6 in different ways.
If 1 is adjacent to 2, 4 and 6, then which of the following statements is necessarily true?
Options- A. 2 is opposite to 6
- B. 1 is adjacent to 3
- C. 3 is adjacent to 5
- D. 3 is opposite to 5 Discuss
More questions
Correct Answer: 4
Explanation:
NA
Correct Answer: 4
Explanation:
All the components of Question Figure form Answer Figure(4)
Correct Answer:
Explanation:
Fold the paper from left to right, then from down to up.
or Fold the paper from right to left, then from up to down.
Correct Answer: 3
Explanation:
Except figure (3), in all other figures the three designs have been shaded differently.
Correct Answer: 3
Correct Answer: 3
Explanation:
Correct Answer: 2
Explanation:
According to above given figure , we can see that
The mirror image always be opposite to the original image across the given line. While given image will become opposite to the given mirror MN.
Correct Answer: 3
Explanation:
The three small circles get arranged in the middle of the triangle and three lines extend from the three vertices of the triangle.
Correct Answer: 14
Explanation:
On the basis of following pattern in given dices , we can say that
Ten block are visible and four block are invisible.
From the diagram it is clear that there are 14 blocks.
Correct Answer: 3 is adjacent to 5
Explanation:
Comments
There are no comments.Programming
Copyright ©CuriousTab. All rights reserved.
