Discussion
Home ‣ Non Verbal Reasoning ‣ Cubes and Dice See What Others Are Saying!
- Question
- How many of the cubes have 0 faces painted?
Options- A. 64
- B. 150
- C. 240
- D. None of these
- Correct Answer
- 150
ExplanationOut of 6 faces of 5 faces are exposed and those were painted.
Number of vertices with three faces exposed (Painted) is 4
Number of vertices with 2 faces exposed (Painted) is 4
Number of vertices with 1 faces exposed (Painted) is 0
Number of vertices with 0 faces exposed (Painted) is 0
Number of sides with 2 sides exposed (Painted) is 8
Number of sides with 1 sides exposed (Painted) is 4
Number of sides with no sides exposed (Painted) is 0
From the above observation:
Number of cubes with 3 faces Painted is 4
Number of cubes with 2 faces Painted is given by sides which is exposed from two sides, out of 8 such edges 4 vertical edges will give us 6 cubes per edge and 4 edges from top surface will give us 5 such cubes from each edge and required number of cubes is 6 x 4 + 4 x 5 = 44.
Number of cubes with 1 face Painted is given by faces which is exposed from one sides four vertical faces will give us 6 x 5 = 30 cubes per face and top face will give us 5 x 5 = 25 and required number of cubes is 30 x 4 + 25 x 1 = 145
Number of cubes with 0 face Painted is given by difference between total number of cubes - number of cubes with at least 1 face painted = 343 - 4 - 44 - 145 = 150
In other words number of cubes with 0 painted is 6 x 5 x 5 = 150
From the above explanation number of the cubes with 0 faces painted is 150. - 1. Select the alternative which represents three out of the five alternative figures which when fitted into each other would form a complete square.

Options- A. 134
- B. 145
- C. 125
- D. 124 Discuss
- 2. Find the question mark ? figure from answer figure.
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 3. NA
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 4. In each of the following questions which of the answer figures is exactly the mirror image of the question figure when the mirror is held at the given point
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 5. Select a figure from amongst the Answer Figures which will continue the same series as established by the five Problem Figures.
Problem Figures: Answer Figures:
 (A) (B) (C) (D) (E) (1) (2) (3) (4) (5)
(A) (B) (C) (D) (E) (1) (2) (3) (4) (5)
Options- A. 1
- B. 2
- C. 3
- D. 4
- E. 5 Discuss
- 6. Identify the figure that completes the pattern.
 (X) (1) (2) (3) (4)
(X) (1) (2) (3) (4)
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 7. CAT2015
Options- A. .
- B. .
- C. .
- D. . Discuss
- 8. A piece of paper is folded and cut as shown below in the question figures. From the given answer figures, indicate how it will appear when opened.
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 9. NA
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 10. Choose a figure which would most closely resemble the unfolded form of Figure (Z).
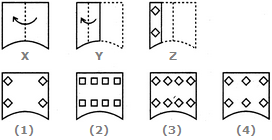
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
More questions
Correct Answer: 145
Explanation:

Correct Answer: 2
Explanation:
From first figure to second figure one box each is deleted from all the four sides.
Correct Answer: 1
Explanation:
NA
Correct Answer: 3
Explanation:
As per the given above question figure ,
Figure ( 3 ) of the answer figures is exactly the mirror image of the given original image across the given line , Because given image will become opposite to the given line MN.So , correct answer is option C .
Correct Answer: 4
Explanation:
Correct Answer: 3
Explanation:

Correct Answer: .
Explanation:
Answer C
Correct Answer: 3
Explanation:
NA
Correct Answer: 2
Explanation:
NA
Correct Answer: 3
Comments
There are no comments.Programming
Copyright ©CuriousTab. All rights reserved.
