Discussion
Home ‣ Non Verbal Reasoning ‣ Cubes and Dice See What Others Are Saying!
- Question
- How many of the cubes have 0 faces painted?
Options- A. 64
- B. 125
- C. 27
- D. None of these
- Correct Answer
- 64
ExplanationSince total number of cubes is hence in the formula we will substitute n = 6
Number of the cubes with 0 faces painted is (6 - 2)3 = 43 = 64 - 1. NA
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 2.
In this question, the sets of numbers given in the alternatives are represented. The columns and rows of Matrix I are numbered from 0 to 4 and that of Matrix II are numbered from 5 to 9. A letter from these matrices can be represented first by its row and next by its column, e.g., 'K' can be represented by 41,34, etc., and 'Z' can be represented by 75, 86, etc. Similarly you have to identify the set for the word 'PAWN'.

Options- A. 44,10,87,55
- B. 99,23,77,59
- C. 03,40,86,65
- D. 31,31,59,66 Discuss
- 3. NA
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 4. Find the question mark ? figure from answer figure.
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 5. Find out the alternative figure which contains figure (X) as its part.
 (X) (1) (2) (3) (4)
(X) (1) (2) (3) (4)
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 6. Choose the figure which is different from the rest.
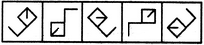 (1) (2) (3) (4) (5)
(1) (2) (3) (4) (5)
Options- A. 1
- B. 2
- C. 3
- D. 4
- E. 5 Discuss
- 7. NA
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 8. NA
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 9. NA
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 10. NA
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
More questions
Correct Answer: 1
Explanation:
After opening the first fold it will look like as:
When it is unfolded completely it will look like as:
Correct Answer: 99,23,77,59
Explanation:
Correct Answer: 3
Explanation:
NA
Correct Answer: 4
Explanation:
From Problem Figure (1) to (2) the design is inverted horizontally. In other words, the second figure is the mirror image of the first figure.
Correct Answer: 3
Explanation:
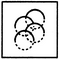
Correct Answer: 3
Explanation:
Correct Answer: 3
Explanation:
NA
Correct Answer: 4
Explanation:
NA
Correct Answer: 4
Explanation:
NA
Correct Answer: 4
Explanation:
NA
Comments
There are no comments.Programming
Copyright ©CuriousTab. All rights reserved.
