Discussion
Home ‣ Electronics and Communication Engineering ‣ Materials and Components See What Others Are Saying!
- Question
If m is the mass of electron cloud, the equation of motion of electron cloud in the presence of an alternating electric field is of the form
Options- A.
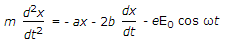
- B.
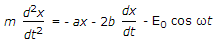
- C.
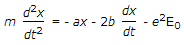
- D.

- Correct Answer
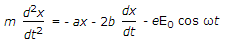
- 1. The final value theorem is
Options- A.
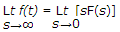
- B.
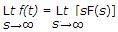
- C.
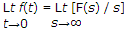
- D.
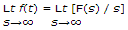 Discuss
Discuss
- 2. Find Vx Vy Vz
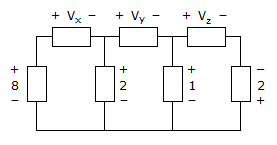
Options- A. Vx = -6 Vy = 3 Vz = -3
- B. Vx = -6 Vy = -3 Vz = 1
- C. Vx = 6 Vy = 3 Vz = 3
- D. Vx = 6 Vy = 1 Vz = 3 Discuss
- 3. In a semiconductor material. The hole concentration is found to be 2 x 2.5 x 1015 cm-3. If mobility of carriers is 0.13 m2/ v-s. Then find the current density if electric field intensity is 3.62 x 10-19
Options- A. 7.6237 x 10-4 A/cm2
- B. 7.6237 x 10-5 A/cm2
- C. 7.6237 x 10-3 A/cm2
- D. none of these Discuss
- 4. The equivalent form of the logical expression ABC + A BC + ABC + ABC + AB C is
Options- A. C + (A ? B)
- B. (A + B + C)(A + B + C)
- C. (A + B + C)(A + B + C)(A + B + C)
- D. (A + B + C)(A + B + C)(A + B + C) Discuss
- 5. Consider the following
- Maximum energy of electrons liberated photoelectrically is independent of light intensity
- Maximum energy of electrons liberated photoelectrically varies nonlinearly with frequency of incident light.
Options- A. (1) is true and (2) is false
- B. (1) and (2) both are true
- C. (1) is false and (2) is true
- D. (1) and (2) both are false Discuss
- 6. The impedance matrices of two, two-port network are given by
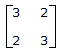 and
and 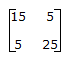 . If these two networks are connected in series, the impedance matrix of the resulting two-port network will be
. If these two networks are connected in series, the impedance matrix of the resulting two-port network will be
Options- A.
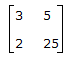
- B.
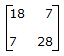
- C.
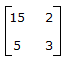
- D. indeterminate Discuss
- 7. For the system of the given figure the transfer function
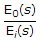 =
=.png)
Options- A.

- B.
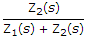
- C.
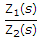
- D.
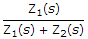 Discuss
Discuss
- 8. If x1[n]
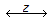 x1(z) with ROC = R1 and x2[n]
x1(z) with ROC = R1 and x2[n] 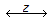 x2(z) with ROC = R2 then ROC for x1[n] + x2[n] will be __________ (where Ri ? Region of convergence and x1[n] and x2[n] are causal).
x2(z) with ROC = R2 then ROC for x1[n] + x2[n] will be __________ (where Ri ? Region of convergence and x1[n] and x2[n] are causal).
Options- A. R1 ? R2
- B. R1 ? R2
- C. (R1 ? R2) ? (R1)
- D. (R1 ? R2) ? (R1) Discuss
- 9. The z-transform of a particular signal is given
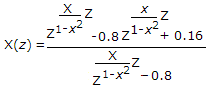 where
where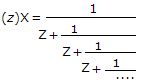
The system after implementation will be
Options- A. casual and stable
- B. non-casual and stable
- C. non-casual and unstable
- D. casual and unstable Discuss
- 10. In a homogeneous magnetic field H of a solenoid, the core carries a magnetic dipole moment M per unit volume equal to
Options- A. ?0 H
- B. ?r H
- C. (?r - 1) H
- D. ?o?r H Discuss
More questions
Correct Answer:
Explanation:

£-1F(s) = f(t)
£[a f1(t) + bf2(t)] = aF1(s) + bF2(s)
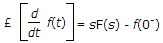
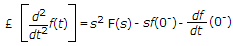

where 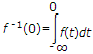
£[f(t - T)] = e-sT F(s)
£[e-at f(t)] = F(s + a)
Initial value theorem 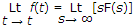
Final value theroem 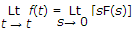
Convolution Integral 

where t is dummy variable for t.
Correct Answer: Vx = 6 Vy = 1 Vz = 3
Explanation:

Apply KVL to mesh 2
-2 + Vy + 1 = 0
? Vy = 1
Apply KVL to mesh 1
? -8 + Vx + 2 = 0
? Vx = 6 V
Apply KVL to mesh 3
-1 + Vz -2 = 0
? Vz = 3 V.
Correct Answer: 7.6237 x 10-4 A/cm2
Explanation:
Where ? = conductivity
Given -> ? = 0.13 m2/v-s = 0.13 x 104 cm2/V sec
P = 2.25 x 1015/cm3
We have, ? ni = 1.5 x 1010
Also n.p. =
? n =  /p
/p

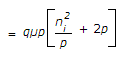
= (1.6 x 10-19 x 0.13 x 104 x 2.25 x 1015) x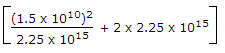
= (0.468) (4.5 x 1015)
? = 2.106 x 1015 ?/cm
J = ?E
? Current density = 2.106 x 1015 x 3.620 x 10-19
= 7.6237 x 10-4 A/m2.
Correct Answer: (A + B + C)(A + B + C)(A + B + C)
Explanation:

(A + B + C) (A + B + C) (A + B + C).
Correct Answer: (1) is true and (2) is false
Explanation:
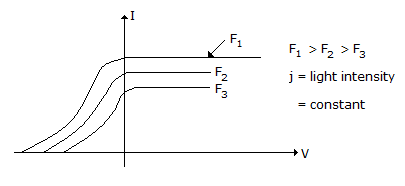
F1 > F2 > F3
j = light intensity = constant
Photocurrent Vs Anode voltage with frequency and incident light as a parameter.
The light intensity is constant.
Correct Answer:
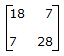
Explanation:
Correct Answer:
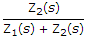
Explanation:
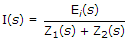 , E0(s) = [I(s)][Z2(s)] or
, E0(s) = [I(s)][Z2(s)] or 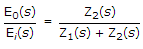 .
.
Correct Answer: R1 ? R2
Explanation:
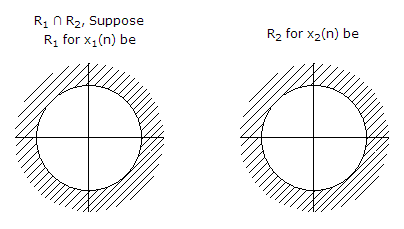
Then ROC for x1(n) + x2(n)
R1 ? R2 (R1 < R2)
Then ROC for x1(n) + x2(n)
R1 ? R2(R1 < R2)

Correct Answer: casual and stable
Explanation:
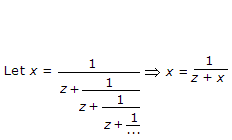
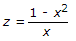
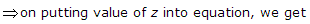
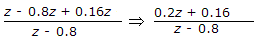
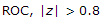
Include unity circle and exterior of circle hence x(z) will be stable, causal.
Correct Answer: (?r - 1) H
Comments
There are no comments.More in Electronics and Communication Engineering:
Programming
Copyright ©CuriousTab. All rights reserved.
