Discussion
Home ‣ Electronics and Communication Engineering ‣ Exam Questions Papers Comments
- Question
If x1[n]
![If x1[n] x1(z) with ROC = R1 and x2[n] x2(z) with ROC = R2 then ROC for x1[n] + x2[n] will be ______](../../../imagesresources/questions-resources/jvtpSxKRhbtUoUSb.png) x1(z) with ROC = R1 and x2[n]
x1(z) with ROC = R1 and x2[n] ![If x1[n] x1(z) with ROC = R1 and x2[n] x2(z) with ROC = R2 then ROC for x1[n] + x2[n] will be ______](../../../imagesresources/questions-resources/jvtpSxKRhbtUoUSb.png) x2(z) with ROC = R2 then ROC for x1[n] + x2[n] will be __________ (where Ri ? Region of convergence and x1[n] and x2[n] are causal).
x2(z) with ROC = R2 then ROC for x1[n] + x2[n] will be __________ (where Ri ? Region of convergence and x1[n] and x2[n] are causal).
Options- A. R1 ? R2
- B. R1 ? R2
- C. (R1 ? R2) ? (R1)
- D. (R1 ? R2) ? (R1)
- Correct Answer
- R1 ? R2
ExplanationR1 ? R2, Suppose R1 for x1(n) be![If x1[n] x1(z) with ROC = R1 and x2[n] x2(z) with ROC = R2 then ROC for x1[n] + x2[n] will be ______](../../../imagesresources/questions-resources/bFFsTGAVnpgFLsKI.png)
Then ROC for x1(n) + x2(n)
R1 ? R2 (R1 < R2)
Then ROC for x1(n) + x2(n)
R1 ? R2(R1 < R2)
![If x1[n] x1(z) with ROC = R1 and x2[n] x2(z) with ROC = R2 then ROC for x1[n] + x2[n] will be ______](../../../imagesresources/questions-resources/cVWaKDtoCAiNxywh.png)
Exam Questions Papers problems
Search Results
- 1. A MOSFET has a threshold voltage of 1 V and oxide thickness of 500 x 10-8 [?r = 3.9; ?0 = 8.85 x 10-14 F/cm, q = 1.6 x 10-19 c]. The region under the gate is ion implanted for threshold voltage tailoring. The base and type of impant required to shift threshold voltage to - 1 V are __________ .
Options- A. 8.6 x 1011/cm2, p-type
- B. 8.6 x 1011/cm2, n-type
- C. 0.86 x 109/cm2, p-type
- D. 1.02 x 1012/cm2, n-type Discuss
Correct Answer: 8.6 x 1011/cm2, p-type
Explanation:
VT(new) = VT(odd) +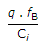
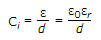
 = 6.903 x 10-8
= 6.903 x 10-8 ?

?

fB = - 8.6 x 1011
The threshold voltage is always negative for p-channel and hence implant is of p-type.
- 2. Suppose that the modulating signal is m(t) = 2cos (2pfmt) and the carrier signal is xC(t) = AC cos(2pfct), which one of the following is a conventional AM signal without over modulation?
Options- A. x(t) = Acm(t)cos(2pfct)
- B. x(t) = Ac [1 + m(t)]cos (2pfct)
- C.

- D. x(t) = Accos(2pfmt)cos(2pfct) + Acsin(2pfmt)sin(2pfct) Discuss
Correct Answer:
Explanation:
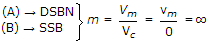
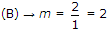
(C) is without over modulation.
- 3. A n-channel JFET has IDSS = 2 mA, Gate to source voltage VGS = - 2 V and trans-conductance is 0.5 mW then pinch-off voltage is __________ .
Options- A. - 2 V
- B. 2 V
- C. - 4 V
- D. 4 V Discuss
Correct Answer: - 4 V
Explanation:

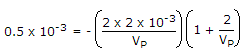
?
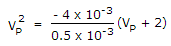
?
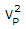 = - 8VP - 16
= - 8VP - 16 ?
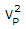 + 8VP + 16 = 0
+ 8VP + 16 = 0 ? (VP + 4)2 = 0
? VP = -4 V.
- 4. What are the values of Emax and Emin displayed on the oscilloscope, when a 1 kV P-P carries is modulated to 50%?
Options- A. 2 kV, 0.5 kV
- B. 1 kV, 0.5 kV
- C. 0.75 kV, 0.25 kV
- D. 0.5 kV, 1.5 kV Discuss
Correct Answer: 0.75 kV, 0.25 kV
Explanation:
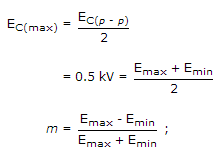
Emax - Emin = 0.5 x 1 kV = 0.5 kV
2Emax = 1.5 kVi, Emax = 0.75 kV
Emin = 0.25 kV.
- 5. If the system T.F. is
 The differential equation representing the system is
The differential equation representing the system is
Options- A.
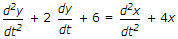
- B.
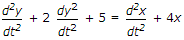
- C.
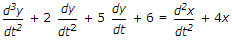
- D. none of these Discuss
Correct Answer: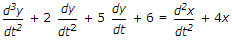
Explanation:
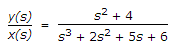
(s3 + 2s2 + 5s + 6)y(s) = (s2 + 4) x (s)
s3y(s) + 2s2y(s) + 5sy(s) + 6y(s) = s2 x (s) + 4 x (s)
Replacing s by
 and y(s) by y(t) and x(s) by x(t) we get
and y(s) by y(t) and x(s) by x(t) we get  y(t) + 2
y(t) + 2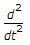 y(t) + 5
y(t) + 5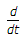 y(t) + 6y(t)
y(t) + 6y(t)=
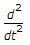 x(t) + 4x(t)
x(t) + 4x(t)  + 2
+ 2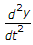 + 5
+ 5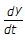 + 6 =
+ 6 = 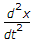 + 4x
+ 4x This is required differential equation.
- 6. If the power spectral density of stationary random process is a sine-squared function of frequency, the shape of its autocorrelation is
Options- A.

- B.

- C.

- D.
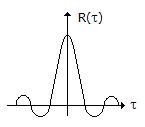 Discuss
Discuss
Correct Answer:
Explanation:
Since autocorrelation function and power spectral density bears a Fourier transform relation, then since required in frequency domain will five rectangular convolutions in time domain thus it is triangular function.- 7. A transmission line has a characteristic impedance of 50 ? and a resistance of 0.1 ?/m, if the line is distortion less, the attenuation constant (in Np/m) is
Options- A. 500
- B. 5
- C. 0.014
- D. 0.002 Discuss
Correct Answer: 0.002
Explanation:
Distortion less
a = RG and Z0 = RG ?
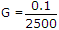
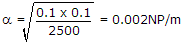 .
.
- 8. Consider a stable and causal system with impulse response h(t) and system function H(S). Suppose H(S) is rational, contains a pole at S = - 2, and does not have a zero at the origin. The location of all other poles and zero is unknown for each of the following statements. Let us determine whether statement is true or false.
- f[h(t) e-3t] converges
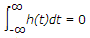
- h(t) has finite duration
- H(s) = H(- s)
Options- A. 1 - True, 2 - False, 3 - True, 4 - False
- B. 1 - False, 2 - False, 3 - False, 4 - True
- C. 1 - False, 2 - False, 3 - False, 4 - False
- D. 1 - True, 2 - can't say, 3 - True, 4 - can't say Discuss
Correct Answer: 1 - False, 2 - False, 3 - False, 4 - False
Explanation:
Statement 1 is false, since f{h(t)e3t} corresponds to the value of the Laplace transform of h(t) at s = 3.If this converges, it implies that s = - 3 is in the ROC.
A casual and stable system must always have its ROC to the right of all its poles. However, s = - 3 is not to the right of the pole at s = - 2.
Statement 2 is false, because it is equivalent to stating that H(0) = 0. This contradicts the fact that H(s) does not have a zero at the origin.
Statement 3 is false. If h(t) is of finite duration, then if its Laplace transform has any points in its ROC, ROC must be the entire s-plane.
However, this is not consistent with H(s) having a pole at s = - 2.
Statement 4 is false. If it were true, then H(s) has a pole at s = - 2, it must also have a pole at s = 2.
This is inconsistent with the fact that all the poles of a causal and stable system must be in the left half of the s-plane.
- 9. During transmission over a communicate channel, bit errors occur independently with probability
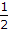 . If a block of 3 bits are transmitted, the probability of at most one bit error is equal to
. If a block of 3 bits are transmitted, the probability of at most one bit error is equal to
Options- A.
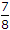
- B.
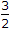
- C.
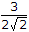
- D. none Discuss
Correct Answer: none
Explanation:
Probability of no-error + probability one error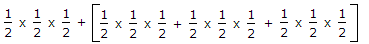
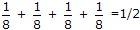 .
.
- 10. Denominator polynomial of a transfer function of certain network is:
s3 + s2 + 2s + 24
Then the network is:
Options- A. stable
- B. oscillatory
- C. unstable
- D. depends on numerator polynomial Discuss
Correct Answer: unstable
Explanation:
Routh array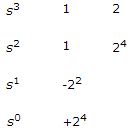
There is negative number present in first column. Thus network is unstable.
Comments
There are no comments.
More in Electronics and Communication Engineering:
Programming
Copyright ©CuriousTab. All rights reserved.
