If toll tax at all of the toll booths is same and is devised such that the ratio

CuriousTab

Discussion

Home ‣ Verbal Reasoning ‣ Routes and Networks See What Others Are Saying!

Question
If toll tax at all of the toll booths is same and is devised such that the ratio of maximum cost to minimum cost of travel from X to Y is 28 : 19 then which one of the following is the cost of travel from X to Y through toll Both T₃?
Options
A. 320 or 510
B. 330 or 560
C. 560 or 510
D. None of these

Correct Answer

560 or 510

Explanation

If toll tax at all of the toll booths is same and let it be k then expense in each path is as follows:
Path 1: 240 + 3k
Path 2: 260 + 5k
Path 3: 260 + 6k
Path 4: 260 + 5k
Path 5: 230 + 3k
So from the given condition On solving we will get k = 50
Tool booth 3 will come in Path 3 and Path 4.
So cost incurred is:
Path 3: 260 + 6k = 260 + 300 = 560
Path 4: 260 + 5k = 260 + 250 = 510
Therefore , 560 or 510 is the cost of travel from X to Y through toll Both T3 .

More questions

4.
Aryabhatta : Mathematician : : Varahamihira :?
Options
A. Physician
B. Astronomer
C. Scientist
D. Architect

Discuss

5.
a. Stem
b. Flower
c. Root
d. Leaves
e. Fruit
Options
A. c, a, d, b, e
B. c, a, e, b, d
C. d, c, a, e, b
D. e, b, a, d, c

Discuss

7.
Statements:
R # T, T � M, M @ D
Conclusions:
I. D S T II. R # M
Options
A. if only conclusion I is true
B. if only conclusion II is true
C. if either conclusion I or conclusion II is true
D. if neither conclusion I nor conclusion II is true

Discuss

8.
Statement:
Should children be prevented completely form using the Internet?
Arguments :
I. No. Internet is a medium of education where children get education with entertainment.
II. Yes. There are some sites available on Internet which show porno film or programmes etc, which affect the child's mind to a great extent; recent surveys have revealed most of the users of these sites are children.
Options
A. if only argument I is strong
B. if only argument II is strong
C. if either I or II is strong
D. if neither I nor II is strong; and

Discuss

9.
Which one of the given responses would be a meaningful order of the following?
1. Epilogue
2. Chapter
3. Index
4. Prologue
5. Cover
Options
A. 3, 4, 2, 1, 5
B. 5, 3, 4, 2, 1
C. 1, 5, 2, 4, 3
D. 1, 3, 4, 2, 5

Discuss

10. The figure given on the left hand side in each of the following questions is folded to form a box. Choose from the alternatives (1), (2), (3) and (4) the boxes that is similar to the box formed.
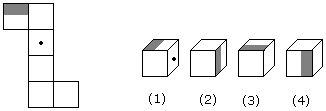
Options
A. 1 and 2 only
B. 2 and 3 only
C. 1, 2, 3 and 4
D. 2 and 4 only

Discuss

Comments

CuriousTab

CuriousTab

Discussion

If toll tax at all of the toll booths is same and is devised such that the ratio of maximum cost to minimum cost of travel from X to Y is 28 : 19 then which one of the following is the cost of travel from X to Y through toll Both T₃?

More questions

More in Verbal Reasoning:

Aptitude

Engineering

Programming

Reasoning

Links

CuriousTab

CuriousTab

Discussion

If toll tax at all of the toll booths is same and is devised such that the ratio of maximum cost to minimum cost of travel from X to Y is 28 : 19 then which one of the following is the cost of travel from X to Y through toll Both T3?

More questions

More in Verbal Reasoning:

Aptitude

Engineering

Programming

Reasoning

Links

Social

If toll tax at all of the toll booths is same and is devised such that the ratio of maximum cost to minimum cost of travel from X to Y is 28 : 19 then which one of the following is the cost of travel from X to Y through toll Both T₃?