logo

CuriousTab

CuriousTab

Discussion

Home ‣ Logical Reasoning ‣ Logical Deduction See What Others Are Saying!
  • Question

  • Statements: All trains are buses. No room is bus. All boats are rooms.

    Conclusions:

    1. No boat is train.
    2. No bus is boat.
    3. No train is room.


  • Options
  • A. None follows
  • B. Only I and II follow
  • C. Only II and III follow
  • D. Only I and III follow
  • E. All follow

  • Correct Answer
  • All follow 

    Explanation
    All trains are buses. No room is bus.

    Since both the premises are universal and one premise is negative, the conclusion must be universal negative (E-type) and should not contain the middle term. So, it follows that 'No train is room'. Thus, III follows.

    All boats are rooms. No room is bus.

    As discussed above, it follows that 'No boat is bus'.

    II is the converse of this conclusion and so it holds. All trains are buses. No boat is bus.

    Again, it follows that 'No train is boat'. I is the converse of this conclusion and so it holds.

    More questions

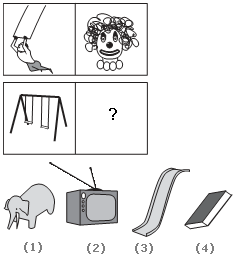
    • 1. Choose the picture that would go in the empty box so that the two bottom pictures are related in the same way as the top two:

    • Options
    • A. 1
    • B. 2
    • C. 3
    • D. 4
      • Discuss
    • 2. Statements: Some dreams are nights. Some nights are days.

      Conclusions:

      1. All days are either nights or dreams.
      2. Some days are nights.


    • Options
    • A. Only conclusion I follows
    • B. Only conclusion II follows
    • C. Either I or II follows
    • D. Neither I nor II follows
    • E. Both I and II follow
      • Discuss
    • 3. Statement: Why don't you invite Anthony for the Christmas party this year?

      Assumptions:

      1. Anthony is not from the same city.
      2. Unless invited Anthony will not attend the party.


    • Options
    • A. Only assumption I is implicit
    • B. Only assumption II is implicit
    • C. Either I or II is implicit
    • D. Neither I nor II is implicit
    • E. Both I and II are implicit
      • Discuss
    • 4. Look at this series: 2, 1, (1/2), (1/4), ... What number should come next?

    • Options
    • A. (1/3)
    • B. (1/8)
    • C. (2/8)
    • D. (1/16)
      • Discuss
    • 5. book

    • Options
    • A. fiction
    • B. pages
    • C. pictures
    • D. learning
      • Discuss
    • 6. Statements: Some tables are TVs. Some TVs are radios.

      Conclusions:

      1. Some tables are radios.
      2. Some radios are tables.
      3. All radios are TVs.
      4. All TVs are tables.


    • Options
    • A. None follows
    • B. All follow
    • C. Only I and III follow
    • D. Only II and IV follow
      • Discuss
    • 7. Statements: Some tigers are lions. Some lions are rabbits. Some rabbits are horses.

      Conclusions:

      1. Some tigers are horses.
      2. Some rabbits are tigers.
      3. Some horses are lions.
      4. All horses are rabbits.


    • Options
    • A. All follow
    • B. None follows
    • C. Only I and II follow
    • D. Only II and IV follow
    • E. Only IV follows
      • Discuss
    • 8. Which word does NOT belong with the others?

    • Options
    • A. branch
    • B. dirt
    • C. leaf
    • D. root
      • Discuss
    • 9. pain

    • Options
    • A. cut
    • B. burn
    • C. nuisance
    • D. hurt
      • Discuss
    • 10. champion

    • Options
    • A. running
    • B. swimming
    • C. winning
    • D. speaking
      • Discuss

    Comments

    There are no comments.
Enter a new Comment




Aptitude

Engineering

Programming

Reasoning

Links

Copyright ©CuriousTab. All rights reserved.