Discussion
Home ‣ Electronics and Communication Engineering ‣ Exam Questions Papers See What Others Are Saying!
- Question
Denominator polynomial of a transfer function of certain network is:
s3 + s2 + 2s + 24
Then the network is:
Options- A. stable
- B. oscillatory
- C. unstable
- D. depends on numerator polynomial
- Correct Answer
- unstable
ExplanationRouth array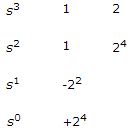
There is negative number present in first column. Thus network is unstable.
More questions
- 1. A class A chopper has an input voltage of 200 V. Ton = 1.5 ms and Toff = 4.5 ms. The duty cycle, average output voltage and ripple factor respectively are
Options- A. 0.5, 100 V and 1
- B. 0.25, 50 V and 3
- C. 0.25, 50 V and 1
- D. 0.5, 100 V and 3 Discuss
Correct Answer: 0.25, 50 V and 3
- 2. The velocity factor of a transmission line depends on
Options- A. temperature
- B. skin effect
- C. relative permittivity of dielectric
- D. none of the above Discuss
Correct Answer: relative permittivity of dielectric
Explanation:
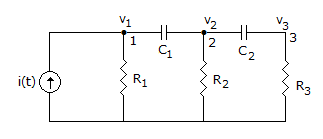
?r of a dielectric changes with humidity.- 3. For node 1 in figure, KCL equation is
Options- A.
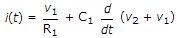
- B.
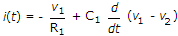
- C.
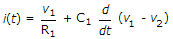
- D. none of the above Discuss
Correct Answer: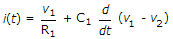
Explanation:
i(t) is the incoming current. The currents leaving node 1 are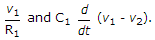
- 4. Maxterm designation for A + B + C is
Options- A. M0
- B. M1
- C. M3
- D. M4 Discuss
Correct Answer: M0
Explanation:
A + B + C = 000 = M0 .- 5. Expression ++i is equivalent to
Options- A. i = i + 2
- B. i = i + 1
- C. i = i - 1
- D. i = i + i + i Discuss
Correct Answer: i = i + 1
Explanation:
i is incremented by 1.- 6. An LVDT is used to measure displacement. The LVDT feeds a Voltmeter of 0-5 V range through a 250 gain amplifier. For a displacement 0.5 mm the output of LVDT is 2 mV. The sensitivity of instrument is
Options- A. 0.1 V/mm
- B. 0.5 V/mm
- C. 1 V/mm
- D. 5 V/mm Discuss
Correct Answer: 1 V/mm
Explanation:
Final output = 2 x 10-3 x 250 = 0.5 V.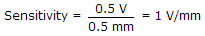 .
.
- 7. Consider the following statement: In case of a superconductor
- B = 0
- ?r is high
- diamagnetism is high
- transition temperature varies with isotopic mass.
Options- A. 1 and 2 are correct
- B. 2, 3, 4 are correct
- C. 1, 3, 4 are correct
- D. 2, 4 are correct Discuss
Correct Answer: 1, 3, 4 are correct
- 8. An electron (charge -e) is rotating in a circular orbit of radius R, around a proton with charge +e at a constant angular velocity ?. The orbital magnetic dipole moment is
Options- A. 0.5 e? R2
- B. e? R2
- C. 2 e? R2
- D. 0.5 e? R3 Discuss
Correct Answer: 0.5 e? R2
- 9. For a given value (n) of principle quantum number, the number of possible electronic states are
Options- A. n
- B. n2
- C. n3
- D. n Discuss
Correct Answer: n2
Explanation:
The total number of states corresponding to a given value of n is equal to (2l + 1) = 1 + 3 + .... + [2(n-1) + 1] = n2.
(2l + 1) = 1 + 3 + .... + [2(n-1) + 1] = n2.
- 10. A dielectric of relative permittivity ?r is subjected to a homogeneous electric field E. The dipole moment P per unit volume is given by
Options- A. P = constant
- B. P = ?0 E
- C. P = ?0(?r - 1) E
- D. P = ?r E Discuss
Correct Answer: P = ?0(?r - 1) E
Comments
There are no comments.
More in Electronics and Communication Engineering:
Programming
Copyright ©CuriousTab. All rights reserved.
