logo

CuriousTab

CuriousTab

Discussion

Home ‣ Electronics and Communication Engineering ‣ Signals and Systems Comments
  • Question

  • The final value theorem is


  • Options
  • A. The final value theorem is £f(t) = £-1F(s) = f(t) £[a f1(t) + bf2(t)] = aF1(s) + bF2(s) where £[f(t
  • B. The final value theorem is £f(t) = £-1F(s) = f(t) £[a f1(t) + bf2(t)] = aF1(s) + bF2(s) where £[f(t
  • C. The final value theorem is £f(t) = £-1F(s) = f(t) £[a f1(t) + bf2(t)] = aF1(s) + bF2(s) where £[f(t
  • D. The final value theorem is £f(t) = £-1F(s) = f(t) £[a f1(t) + bf2(t)] = aF1(s) + bF2(s) where £[f(t

  • Correct Answer
  •  

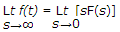
    Explanation
    £f(t) = The final value theorem is £f(t) = £-1F(s) = f(t) £[a f1(t) + bf2(t)] = aF1(s) + bF2(s) where £[f(t

    £-1F(s) = f(t)

    £[a f1(t) + bf2(t)] = aF1(s) + bF2(s)

    The final value theorem is £f(t) = £-1F(s) = f(t) £[a f1(t) + bf2(t)] = aF1(s) + bF2(s) where £[f(t

    The final value theorem is £f(t) = £-1F(s) = f(t) £[a f1(t) + bf2(t)] = aF1(s) + bF2(s) where £[f(t

    The final value theorem is £f(t) = £-1F(s) = f(t) £[a f1(t) + bf2(t)] = aF1(s) + bF2(s) where £[f(t

    where The final value theorem is £f(t) = £-1F(s) = f(t) £[a f1(t) + bf2(t)] = aF1(s) + bF2(s) where £[f(t

    £[f(t - T)] = e-sT F(s)

    £[e-at f(t)] = F(s + a)

    Initial value theorem The final value theorem is £f(t) = £-1F(s) = f(t) £[a f1(t) + bf2(t)] = aF1(s) + bF2(s) where £[f(t

    Final value theroem The final value theorem is £f(t) = £-1F(s) = f(t) £[a f1(t) + bf2(t)] = aF1(s) + bF2(s) where £[f(t

    Convolution Integral The final value theorem is £f(t) = £-1F(s) = f(t) £[a f1(t) + bf2(t)] = aF1(s) + bF2(s) where £[f(t

    The final value theorem is £f(t) = £-1F(s) = f(t) £[a f1(t) + bf2(t)] = aF1(s) + bF2(s) where £[f(t

    where t is dummy variable for t.

    Signals and Systems problems

    Search Results

    • 1. The z-transform of a particular signal is given
      where

      The system after implementation will be

    • Options
    • A. casual and stable
    • B. non-casual and stable
    • C. non-casual and unstable
    • D. casual and unstable
      • Discuss
    • 2. Laplace transform of a pulse function of magnitude E and duration from t = 0 to t = a is

    • Options
    • A. E / s
    • B.
    • C.
    • D.
      • Discuss
    • 3. Inverse Laplace transform of is

    • Options
    • A. 2 exp (- 2.5 t) cosh (0.5 t)
    • B. exp (- 2 t) + exp (- 3 t)
    • C. 2 exp (- 2.5 t) sinh (0.5 t)
    • D. 2 exp (- 2.5 t) cos 0.5 t
      • Discuss
    • 4. Which one most appropriate dynamic system?

    • Options
    • A. y(n) + y(n - 1) + y(n + 1)
    • B. y(n) + y(n - 1)
    • C. y(n) = x(n)
    • D. y(n) + y(n - 1) + y(n + 3) = 0
      • Discuss
    • 5. ?(t) is a

    • Options
    • A. energy signal
    • B. power signal
    • C. neither energy nor power
    • D. none
      • Discuss
    • 6. Which one is a causal system?

    • Options
    • A. y(n) = 3x[n] - 2x[n - 1]
    • B. y(n) = 3x[n] + 2x[n + 1]
    • C. y(n) = 3x[n + 1] + 2x[n - 1]
    • D. y(n) = 3x[n + 1] 2x[n - 1] + x[n]
      • Discuss
    • 7. A signal g(t) = A then g(t) is a

    • Options
    • A. energy signal
    • B. power signal
    • C. neither energy nor power signal
    • D. insufficient data
      • Discuss
    • 8. A box has 4 white and 3 red balls. Two balls are taken out in succession. What is the probability that both are white?

    • Options
    • A.
    • B.
    • C.
    • D.
      • Discuss
    • 9. If and A + B is

    • Options
    • A.
    • B.
    • C.
    • D.
      • Discuss
    • 10. In Laplace transform, multiplication by e-at in time domain becomes

    • Options
    • A. translation by a in s domain
    • B. translation by (-a) in s domain
    • C. multiplication by e-as in s domain
    • D. none of the above
      • Discuss

    Comments

    There are no comments.
Enter a new Comment




Aptitude

Engineering

Programming

Reasoning

Links

Copyright ©CuriousTab. All rights reserved.