Discussion
Home ‣ Logical Reasoning ‣ Logical Deduction Comments
- Question
Statements: Some desks are caps. No cap is red.
Conclusions:
- Some caps are desks.
- No desk is red.
Options- A. Only conclusion I follows
- B. Only conclusion II follows
- C. Either I or II follows
- D. Neither I nor II follows
- E. Both I and II follow
- Correct Answer
- Only conclusion I follows
ExplanationSince one premise is particular and the other premise is negative, the conclusion must be particular negative and should not contain the middle term. So, it follows that 'Some desks are not red'. However, I is the converse of the first premise and thus it holds. - 1. Statements: Raman is always successful. No fool is always successful.
Conclusions:
- Raman is a fool.
- Raman is not a fool.
Options- A. Only conclusion I follows
- B. Only conclusion II follows
- C. Either I or II follows
- D. Neither I nor II follows
- E. Both I and II follow Discuss
- 2. Statements: All trucks fly. Some scooters fly.
Conclusions:
- All trucks are scooters.
- Some scooters do not fly.
Options- A. Only conclusion I follows
- B. Only conclusion II follows
- C. Either I or II follows
- D. Neither I nor II follows
- E. Both I and II follow Discuss
- 3. Statements: Some books are tables. Some tables are mirrors.
Conclusions:
- Some mirrors are books.
- No book is mirror.
Options- A. Only conclusion I follows
- B. Only conclusion II follows
- C. Either I or II follows
- D. Neither I nor II follows
- E. Both I and II follow Discuss
- 4. Statements: All huts are mansions. All mansions are temples.
Conclusions:
- Some temples are huts.
- Some temples are mansions.
Options- A. Only conclusion I follows
- B. Only conclusion II follows
- C. Either I or II follows
- D. Neither I nor II follows
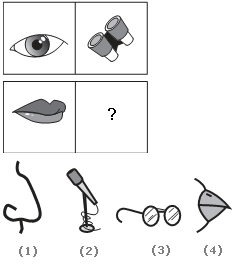
- E. Both I and II follow Discuss
- 5. Statements: No magazine is cap. All caps are cameras.
Conclusions:
- No camera is magazine.
- Some cameras are magazines.
Options- A. Only conclusion I follows
- B. Only conclusion II follows
- C. Either I or II follows
- D. Neither I nor II follows
- E. Both I and II follow Discuss
- 6. Statements: Some hens are cows. All cows are horses.
Conclusions:
- Some horses are hens.
- Some hens are horses.
Options- A. Only conclusion I follows
- B. Only conclusion II follows
- C. Either I or II follows
- D. Neither I nor II follows
- E. Both I and II follow Discuss
- 7. Statements: All water is divine. All temples are divine.
Conclusions:
- All water is temple.
- All temples are water.
Options- A. Only conclusion I follows
- B. Only conclusion II follows
- C. Either I or II follows
- D. Neither I nor II follows
- E. Both I and II follow Discuss
- 8. Statements: All men are dogs. All dogs are cats.
Conclusions:
- All men are cats.
- All cats are men.
Options- A. Only conclusion I follows
- B. Only conclusion II follows
- C. Either I or II follows
- D. Neither I nor II follows
- E. Both I and II follow Discuss
- 9. Statements: All young scientists are open-minded. No open-minded men are superstitious.
Conclusions:
- No scientist is superstitious.
- No young people are superstitious.
Options- A. Only conclusion I follows
- B. Only conclusion II follows
- C. Either I or II follows
- D. Neither I nor II follows
- E. Both I and II follow Discuss
- 10. Statements: Some pastries are toffees. All toffees are chocolates.
Conclusions:
- Some chocolates are toffees.
- Some toffees are not pastries.
Options- A. Only conclusion I follows
- B. Only conclusion II follows
- C. Either I or II follows
- D. Neither I nor II follows
- E. Both I and II follow Discuss
Logical Deduction problems
Search Results
Correct Answer: Only conclusion II follows
Explanation:
Since both the premises are universal and one premise is negative, the conclusion must be universal negative and should not contain the middle term. So, only II follows.
Correct Answer: Neither I nor II follows
Explanation:
Since the middle term 'fly' is not distributed even once in the premises, no definite conclusion follows.
Correct Answer: Either I or II follows
Explanation:
Since both the premises are particular no definite conclusion follows. However, I and II involve only the extreme terms and form a complementary pair. Thus, either I or II follows.
Correct Answer: Both I and II follow
Explanation:
As discussed above, it follows that 'All huts are temples'. I is the converse of this conclusion and so it holds. II is the converse of the second premise and so it also holds.
Correct Answer: Either I or II follows
Explanation:
As discussed above, the conclusion must be particular negative and should not contain the middle term. So, it follows that 'Some cameras are not magazines'. However, I and II involve only the extreme terms and form a complementary pair. Thus, either I or II follows.
Correct Answer: Both I and II follow
Explanation:
Since one premise is particular, the conclusion must be particular and should not contain the middle term. So, II follows. I is the converse of II and so it also holds.
Correct Answer: Neither I nor II follows
Explanation:
Since the middle term 'divine' is not distributed even once in the premises, no definite conclusion can be drawn.
Correct Answer: Only conclusion I follows
Explanation:
Since both the premises are universal and affirmative, the conclusion must be universal affirmative. However, conclusion II, being an A-type proposition, distributes the term 'cats'.
Since the term 'cats' is distributed in II without being distributed in any of the premises, so conclusion II cannot follow. Thus, only I follows.
Since the term 'cats' is distributed in II without being distributed in any of the premises, so conclusion II cannot follow. Thus, only I follows.
Correct Answer: Neither I nor II follows
Explanation:
The subject in both the conclusions is vague. The true conclusion is 'No young scientist is superstitious'. Thus, neither I nor II follows,
Correct Answer: Only conclusion I follows
Explanation:
Since one premise is particular, the conclusion must be particular and should not contain the middle term. Thus, it follows that 'Some pastries are chocolates', I is the converse of the second premise and so it holds. Since both the premises are affirmative, the conclusion cannot be negative. Thus, II does not follow.
Comments
There are no comments.More in Logical Reasoning:
Programming
Copyright ©CuriousTab. All rights reserved.