Discussion
Home ‣ Logical Reasoning ‣ Statement and Conclusion See What Others Are Saying!
- Question
I. a2-7a+12 = 0 , II. b2-3b+2 = 0 Solve both the equations to find the values of a and b ?
Options- A. if a > b
- B. if a < b
- C. if the relationship between a and b cannot be established.
- D. if a ? b
- Correct Answer
- if a > b
ExplanationI. (a - 3)(a - 4) = 0
=> a = 3, 4
II. (b - 2)(b - 1) = 0
=> b = 1, 2
=> a > b
- 1. Statement: Children are influenced more by their teachers nowadays.
Assumptions:
- The children consider teachers as their models.
- A large amount of children's time is spent in school.
Options- A. Only assumption I is implicit
- B. Only assumption II is implicit
- C. Either I or II is implicit
- D. Neither I nor II is implicit
- E. Both I and II are implicit Discuss
- 2. Most Reality TV centers on two common motivators: fame and money. The shows transform waitresses, hairdressers, investment bankers, counselors, and teachers, to name a few, from obscure figures to house-hold names. A lucky few successfully parlay their fifteen minutes of fame into celebrity. The luckiest stars of Reality TV also reap huge financial rewards for acts including eating large insects, marrying someone they barely know, and revealing their innermost thoughts to millions of people.
This paragraph best supports the statement that
Options- A. the stars of Reality TV are interested in being rich and famous.
- B. Reality TV is the best thing that has happened to network television in a long time.
- C. for Reality TV stars, fame will last only as long as their particular television show.
- D. traditional dramas and sitcoms are being replaced by Reality TV programming at an alarming rate.
- E. Reality TV shows represent a new wave of sensationalistic, low quality programming. Discuss
- 3. Which word does NOT belong with the others?
Options- A. book
- B. index
- C. glossary
- D. chapter Discuss
- 4. 42 40 38 35 33 31 28
Options- A. 25 22
- B. 26 23
- C. 26 24
- D. 25 23
- E. 26 22 Discuss
- 5. Look at this series: 1.5, 2.3, 3.1, 3.9, ... What number should come next?
Options- A. 4.2
- B. 4.4
- C. 4.7
- D. 5.1 Discuss
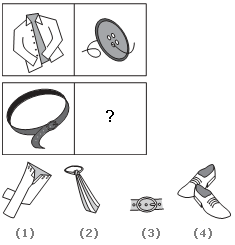
- 6. Choose the picture that would go in the empty box so that the two bottom pictures are related in the same way as the top two:
Options- A. 1
- B. 2
- C. 3
- D. 4 Discuss
- 7. Which word does NOT belong with the others?
Options- A. couch
- B. rug
- C. table
- D. chair Discuss
- 8. Which word does NOT belong with the others?
Options- A. eel
- B. lobster
- C. crab
- D. shrimp Discuss
- 9. 14 14 26 26 38 38 50
Options- A. 60 72
- B. 50 62
- C. 50 72
- D. 62 62
- E. 62 80 Discuss
- 10. All guilty politicians were arrested. Kishan and Chander were among those arrested.
Options- A. All politicians are guilty.
- B. All arrested people are politicians.
- C. Kishan and Chander were not politicians.
- D. Kishan and Chander were guilty. Discuss
More questions
Correct Answer: Only assumption I is implicit
Explanation:
Clearly, it is because children consider teachers as their model that they are more influenced by them. So, I is implicit. It is not necessary that the children are influenced by teachers because they spend much time in school. So, II is not implicit.
Correct Answer: the stars of Reality TV are interested in being rich and famous.
Explanation:
This is expressed in the first sentence. Choices b, d, and e are not supported by the passage. Choice c is incorrect because the paragraph states that some Reality TV stars manage to parlay their fifteen minutes of fame into celebrity.
Correct Answer: book
Explanation:
An index, glossary, and chapter are all parts of a book. Choice a does not belong because the book is the whole, not a part.
Correct Answer: 26 24
Explanation:
This is an alternating subtraction series in which 2 is subtracted twice, then 3 is subtracted once, then 2 is subtracted twice, and so on.
Correct Answer: 4.7
Explanation:
In this simple addition series, each number increases by 0.8.
Correct Answer: 3
Explanation:
A shirt is to a button as a belt is to a belt buckle. A button is used to close a shirt; a belt buckle is used to close a belt.
Correct Answer: rug
Explanation:
The couch, table, and chair are pieces of furniture; the rug is not.
Correct Answer: eel
Explanation:
The lobster, crab, and shrimp are all types of crustaceans; an eel is a fish.
Correct Answer: 50 62
Explanation:
In this simple addition with repetition series, each number in the series repeats itself, and then increases by 12 to arrive at the next number.
Correct Answer: Kishan and Chander were guilty.
Comments
There are no comments.More in Logical Reasoning:
Programming
Copyright ©CuriousTab. All rights reserved.
